Improving Pump Efficiency

As energy costs rise, equipment suppliers, system designers, and operators focus increasingly on maximizing the efficiency of HVAC-system components to conserve energy and reduce operating expenses. This article discusses methods of achieving more-efficient pumping systems.

Examine the System

In designing a pumping system, one needs to look beyond the pumps, if energy savings are to be achieved. Also of importance are:

• The boiler, chiller, or heat exchanger.

• Pipe size and design.

• Elements Affecting Pump Operating Efficiency

  Valve losses.

• Radiation efficiency.

• In a heating system, water temperature, which should vary with outside temperature to reduce heating/cooling costs.

• Motor efficiency, pump size, and the use of variable-speed controls.

• Operating point.

A pump loses energy because of friction related to piping and fittings, heat exchangers, heating/cooling coils, control valves, and balance valves. If friction can be minimized, pump size can be reduced and energy saved. For instance, instead of using on/off valves and balancing valves, design piping in a primary/secondary configuration with the coils in the secondary loop, and turn on a low-energy pump only when needed. The main circulation pump can be low energy because it does not have to overcome control-valve-related friction.

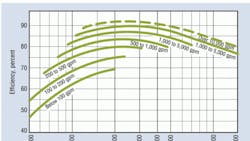
Most centrifugal-pump manufacturers specify performance based on the pumping of clear 68°F water. The major influences on centrifugal-pump efficiency are specific speed, pump size, net positive suction head (NPSH) available and NPSH required, viscosity of the fluids being pumped, temperature, specific gravity, and pump type. The Hydraulic Institute has charted the expected efficiency of different types of pumps at different specific speeds. Specific speed is a dimensionless number calculated from the formula:

N × Q^.5 ÷ H^.75

where:

N = revolutions per minute

Q = flow, gallons per minute

H = head, feet of water

A circulator producing 20 gpm and 20 ft of head at 1,725 rpm has a specific speed of 816. A pump producing 5,000 gpm and 150 ft of head at 1,750 rpm has a specific speed of 2,887. Pump efficiency at the optimum specific speed of 816 is 30 percent; the correction factor is 5 percent. The predicted efficiency of 30 percent minus 5 percent is 25 percent. The normal deviation is ±16 percent, so this pump's predictive efficiency is 9 to 14 percent.

The high-flow-and-head pump would have an optimum generally attainable efficiency of 89 percent with no correction factor. The deviation from attainable efficiency is 3 percent. From these calculations, one can see the efficiency of pumps with low head and low flow is low, while the efficiency of pumps with high flow and high head is high. In high-specific-speed pumps, the deviation is much smaller.

Factors affecting deviation from attainable efficiency are surface roughness; internal clearances; mechanical losses, such as those related to bearings, lip seals, mechanical seals, and packing; high suction specific speed; impeller trim; and the viscosity of the fluid pumped. Low-specific-speed pumps are affected most by surface roughness, internal clearances, and mechanical losses. High-specific-speed pumps are affected most by high-suction-speed requirements, impeller trim, and viscosity.

Page 2 of 2

Centrifugal Pumps and BEP

Best efficiency point (BEP) is the head, flow, and speed at which a centrifugal pump is designed for optimal performance. A pump should be selected so that it always operates near its BEP. Operating a pump at less than or more than its BEP will lower the operational efficiency and place additional stress on the pump shaft and bearing because of increased thrust and radial load. Higher flows increase required NPSH and may result in erosion attributed to cavitation, as well as increased noise and vibration.

Pumps are variable-torque machines that follow the affinity laws. The affinity laws predict changes in pump performance resulting from changes in speed or impeller diameter. If pump performance is unnecessarily high, energy savings can be achieved through use of a variable-speed drive or the matching of impeller trim to system resistance. Throttling adds resistance to a system, but is not as efficient as reducing speed or impeller diameter.

The affinity laws are:

(rpm₂ ÷ rpm₁) × gpm₁ = gpm₂

(rpm₂ ÷ rpm₁)² × H₁ = H₂

(rpm₂ ÷ rpm₁)³ × bhp₁ = bhp₂

where:

bhp = brake horsepower

One can see from the last formula that brake horsepower changes with the cube of speed ratio, a significant energy savings for a small change in speed. Reductions in impeller diameter follow the same rules. Reducing impeller diameter decreases head, flow, and brake horsepower. The farther one gets from full-size diameter, the greater the drop in efficiency. This drop in efficiency, however, should be offset by the reduction in horsepower attributed to lower head.

Brake horsepower is calculated as follows:

Q × F × specific gravity of water ÷ 3,960 × pump efficiency

To predict operating cost, we need to take into account the efficiency factor of the electric motor driving the pump:

bhp × 0.746 ÷ motor efficiency = pump kilowatts

(Note: The specific gravity of fluids other than water has an effect on brake horsepower.)

With heating/cooling systems typically operating at full load for only a small portion of a given day, a change in pump speed has a greater effect on energy savings than a few-percentage-point change in pump efficiency. Staging pumps of different sizes, rather than operating a single large pump, may be economical.

Viscosity of Fluids

The viscosity of pumped fluids has a significant effect on pump performance and efficiency. It also has a significant effect on friction loss and heat-transfer rate. It is the responsibility of system designers to supply to pump manufacturers the true flow and head requirements of a system operating with fluids other than water.

Many engineering handbooks have tables and charts for calculating friction loss in pipes and fittings. The Hydraulic Institute's Engineering Data Book (http://bit.ly/hblone) has much information on fluids and loss-calculation methods.

Once fluid flow, resistance (head), temperature, type, and — if it is a mixture of water and another liquid — concentration are calculated, pump size, materials of construction, and motor can be selected. Centrifugal pumps normally pump liquids with viscosities below 3,000 SSU (660 cSt). However, they can pump liquids with viscosities of up to at least 15,000 SSU (3,300 cSt). The higher the viscosity, the more significant the reductions in capacity, head, and efficiency.

The effects of viscosity on the performance of a centrifugal pump operating at its BEP can be seen in Table 1.

ANSI/HI 9.6.7, Effects of Liquid Viscosity on Rotodynamic (Centrifugal and Vertical) Pump Performance, allows the engineer to calculate the performance of a pump more accurately than ever before.

Variable-Speed Pumping

Most HVAC systems are designed to keep a building cool on the hottest days and warm on the coldest days. That being the case, a HVAC system needs to work at full capacity on only the 10 or so hottest and coldest days of the year; for the rest of the year, it should operate at reduced capacity to save energy.

Variable-frequency drives (VFDs) can be used to reduce motor speed and, thus, power consumption when full flow is not required. For example, at 80-percent nominal flow, power consumption is reduced by some 50 percent with a VFD.

Not only does the use of VFDs to control a HVAC system save money — in many instances, the payback period for installing adjustable-frequency drives in place of other flow-control methods is less than 12 months — it increases indoor comfort and reduces equipment-maintenance costs and operational downtime. Plus, should the building be LEED-certified and meet the requirements of the Energy Policy Act of 2005, additional money-saving opportunities are afforded through state- and local-government incentives.

Conclusion

Many factors affect the efficiency of a pumping system. Thus, the whole system needs to be analyzed, not just the pumps. The questions to be answered are: Is this a steady-state system or a cyclic system, and how would the system best operate at off-peak periods, relying on variable-speed pumping, to achieve the highest efficiency?