Fan Selection and Energy Savings
HVAC design engineers face many choices throughout the planning process, perhaps few as crucial as that of fan equipment, a principal consumer of energy. This article will discuss options for improving energy efficiency when designing a HVAC system and selecting a fan.
Power Consumption
Fan power consumption is directly proportional to system flow rate and static pressure. For theoretically perfect efficiency, the minimum power required to move air against resistance is defined as:
AHP = (Q × P) ÷ 6,356
where:
AHP = air horsepower
Q = volumetric flow rate (cubic feet per minute)
P = pressure (inches of water gauge) or resistance
Flow rates are predetermined based on space type and occupancy. Although local codes determine minimum requirements for HVAC systems, ASHRAE Handbook—HVAC Applications1 provides general design criteria for various commercial and public buildings. These criteria include air movement, room circulation, noise, and filter efficiency. Although all are important, room circulation, in air changes per hour, typically determines airflow requirements.
Because flow rate is driven by design criteria, a design engineer's primary means of reducing energy use is to minimize the static pressure needed to move air through a system.
System Pressure Loss
Air Movement and Control Association (AMCA) International defines system pressure loss as "the sum of the static-pressure losses due to friction, shock, dissipation of velocity pressure at the system discharge, and the static-pressure differences between the entry and discharge openings of an air system."2
The static pressure a fan must overcome is dependent on many variables, only some of which the design engineer can control. The location of equipment often is determined by the architect and, therefore, limits the engineer's options.
Duct configuration and fittings used to connect components are large contributors to static pressure. Other sources of system pressure loss are balancing and control dampers, variable-air-volume (VAV) boxes, diffusers, louvers, coils, filters, and other components in an air stream. Given that velocity pressure is proportional to the square of velocity, pressure loss in most of these components is proportional to velocity squared. This makes size an important factor, as cross-sectional area dictates fluid velocity. For example, reducing air velocity throughout a system by 10 percent would result in a 20-percent reduction in system static pressure. With air power proportional to pressure, this would equate to a 20-percent reduction in energy consumption.
In addition to accounting for all static-pressure loss in a system and achieving required room airflow, a design engineer must adhere to Section 6.5.3 of ANSI/ASHRAE/IESNA Standard 90.1, Energy Standard for Buildings Except Low-Rise Residential Buildings, which limits the power (horsepower) a fan can consume per cubic foot per minute of airflow the fan generates. With flow requirements defined, a design engineer must limit system static pressure to meet this power limitation.
System Effect
A major contributor to energy consumption that often is ignored is system effect. AMCA International defines system effect as "a decrease in fan performance capability, observed as a pressure loss, which results from the effect of fan-inlet restrictions/obstructions, fan-outlet restrictions, or other conditions influencing the performance of the fan when it is installed in a system."2 System effect is a reduction in a fan's ability to generate pressure and can be looked at as an additional system pressure loss. It can lead to underperformance, excessive noise, and vibration in a fan and system.
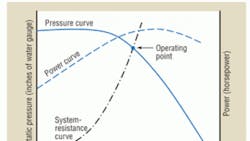
System effect can be described by its impact on a fan curve. Fan curves are produced from laboratory testing, with fans configured for ideal installations. Testing is performed in accordance with ANSI/AMCA Standard 210-07/ANSI/ASHRAE Standard 51-2007, Laboratory Methods of Testing Fans for Certified Aerodynamic Performance Rating. A fan curve displays performance for a constant speed (revolutions per minute) in terms of static pressure vs. volumetric flow rate. In Figure 1, the intersection of the system-resistance curve and the pressure curve is the operating point of the fan. To move along the system curve to alter fan performance, one must increase or decrease fan speed accordingly. Operating power is where the power curve intersects with a vertical line running through the operating point.
The ideal inlet and outlet conditions under which fans are tested rarely are seen in the field. As a result, a fan will overperform or underperform in terms of flow rate, static pressure, or both. In Figure 2, a suitable fan was selected, but system effect was ignored. The blue lines represent how the fan would perform under AMCA International test conditions. Actual measured performance is indicated by the red dot. The red line shows how the fan would perform in an AMCA International air test when operating at design speed, but takes into account system effect. The only way to achieve the desired performance is to speed the fan to the rate designated by the green line. The consequence is a higher operating speed, higher brake horsepower, and higher sound levels.
When moving along a system-resistance curve, a fan's performance will follow the fan laws. The fan laws define the relationships between fan speed, flow rate, static pressure, and horsepower. For constant air density, the equations for these relationships are:
Q2 = Q1 × (N2 ÷ N1)
Ps2 = Ps1 × (N2 ÷ N1)2
H2 = H1 × (N2 ÷ N1)3
where:
1 = "before" state of operation
2 = "after"state of operation
Q = volumetric flow rate (cubic feet per minute)
N = fan speed (revolutions per minute)
Ps = static pressure (inches of water gauge)
H = power consumption (horsepower)
Important to note are that a change in flow is directly proportional to the ratio of a change in fan speed, static pressure is directly proportional to the square of the ratio of a change in fan speed, and power is directly proportional to the cube of the ratio of a change in fan speed. Therefore, when an increase in fan speed is required to overcome system effects, power consumption will go up by a cube of the ratio of "after" fan speed to "before" fan speed.
Even when a non-ideal installation is recognized, system effect is difficult to predict. Installed conditions can vary from design conditions significantly. AMCA Publication 201-02, Fans and Systems,3 provides general guidelines for predicting pressure losses for common system-effect situations. Four sources of system effects often overlooked are:
- Elbows placed at the inlet(s) of a fan.
- Fan inlet in close proximity to a wall.
- Free-discharge situations.
- Rapid transitions at the inlet or discharge of a fan.
Typically, these are the result of limited space.
Non-uniform flow at the inlet of a fan leads to uneven loading of the fan's impeller or wheel. Depending on flow velocity, the straight duct required to avoid system effect between a duct elbow and fan inlet is three to eight times the diameter of the duct in length. If that amount is not possible, larger-radius turns in ductwork and turning vanes are recommended. When a fan has an inlet near a wall or obstruction, open space equivalent to at least one-half the diameter of the fan impeller should be between the wall and fan inlet.
Inability to achieve a uniform airflow-velocity profile before a free discharge or outlet elbow also will result in system effect. Having a run of straight duct at least two-and-a-half times the diameter of the duct in length at the discharge of a fan before a free discharge or elbow is recommended; for every 1,000 fpm of velocity beyond 2,500 fpm, one duct diameter of length should be added. While a free-discharge situation may seem unlikely to have a significant impact, for a single-width-single-inlet centrifugal fan with free discharge and an outlet velocity of 3,000 fpm, the system effect would be equivalent to approximately 0.45 in. wg of static pressure.
To minimize the effects of duct transitions, limit sidewall angles to 7.5 degrees for diverging duct and 30 degrees for converging duct.
Fan Selection
Another key to reducing power consumption is fan selection. Generally, propeller or tube-axial fans are more efficient for relatively low static pressures, while centrifugal-type fans are used for relatively high static pressures.
Too often, fan selection is based solely on first cost. The consequence is that a relatively small-diameter, high-speed fan is used. A small fan operating at a high speed generally requires more operating power and produces more noise than a large fan operating at a low speed.
Fan static efficiency is calculated using the following equation:
ηs = (Q × Ps) ÷ (6,356 × H)
where:
ηs = fan static efficiency
Q = volumetric flow rate (cubic feet per minute)
Ps = fan static pressure (inches of water gauge)
H = operating power (horsepower)
For fans operating at equal flow rate and static pressure, the lower the operating power, the higher the static efficiency.
Peak static efficiency is located near the top of a typical fan curve, as seen in Figure 3. Fans of the same model but different sizes likely have the same or a similar maximum static efficiency. In a comparison of several fans of various sizes for a particular level of performance, the operating points for the smaller-diameter selections will be located farther from the top of the fan curve and peak static efficiency, as seen in Figure 4. In Figure 4, the operating point is closer to the top of the curve of the largest fan; therefore, the fan is functioning closer to the maximum static efficiency. Note that selections near the top of a fan curve offer little factor of safety. A small change in system pressure will result in a large change in flow rate. Variable-volume systems may need to be selected farther to the right on fan curves to ensure stability at reduced airflow.
Take, for example, three centrifugal fans of different sizes selected to operate at 15,000 cfm and a static pressure of 4 in. wg (Table 1). The larger-diameter fans operate at a slower speed and a higher static efficiency and draw less power. Table 2 compares the fans' initial costs and annual operating costs. The operating costs are based on the fans operating 16 hr a day, 365 days a year at an electricity rate of 10 cents per kilowatt-hour. Payback for the 27-in.-diameter fan and the 30-in.-diameter fan compared with the 24-in.-diameter fan is less than one year. For each selection, annual operating cost exceeds initial cost.
Drive Selection
Whether a fan is belt- or direct-driven impacts efficiency.
Belt drives offer the ability to adjust fan speed and balance a system; however, efficiency losses range from a median 15 percent for fractional-horsepower motors to 4 percent for larger motors (Figure 5).4 Additionally, belt-driven fans require regular maintenance. As belts wear, dust accumulates around a fan; in an air handler or makeup-air unit, this causes filters to load faster or, in the absence of filters, compromises air quality.
Because the wheel or impeller is connected directly to the motor shaft, direct-drive fans do not have the losses associated with belt-driven fans. Also, without belts, pulleys, and shaft bearings, they require less maintenance, and, with fewer rotating components, they generally experience less vibration. However, the larger, lower-speed motors associated with larger direct-drive fans generally cost more; thus, return-on-investment calculations should be performed.
Variable-Frequency Drives
Variable-frequency drives (VFDs) are used in both belt-driven and direct-drive systems to maximize energy savings. Reducing input power frequency with a VFD as building load decreases lowers motor speed, airflow, and power. As building occupancy changes, fan speed can be changed and power consumption reduced.
Where Does Lost Energy Go?
Most of the energy lost in a system is converted to heat. For example, mechanical and electrical energy losses in a fan motor raise the surface temperature of the motor. If the motor is in an air stream, the heat will be transferred directly to the air.
In a belt-driven system, losses are the result of belt friction, slippage, and/or flexing. All such losses are converted to heat and, if the belt drive is in an air stream, increase the temperature of air. Fan losses quantified by fan efficiency contribute to air-temperature rise as well. As a fan works on a fluid, the friction attributed to the airflow decreases the fan's efficiency and creates heat.
Figure 6 shows energy transfer in a typical belt-driven fan. The energy flow starts with the power supplied to the motor and ends with the air power generated by the fan. In this example, the motor receives 3,730 W of power, or the equivalent of 5 hp. After losses in the motor, drives, and fan, 2,209 W of air power is delivered. That air power accounts for only 60 percent of the power supplied to the motor. The 1,521 W lost in the process is converted to heat. If the components were located in an air stream, the heat would transfer to and increase the temperature of the air.
As the efficiency of a system decreases, air-temperature rise increases. In a cooling application, this means increased energy consumption on the part of the compressor. Minimizing inefficiencies results in energy savings.
Summary
It is the engineer's responsibility to minimize total system pressure through proper design and layout. This involves balancing economics and efficiencies in specifying a fan.
But not all responsibility resides with the engineer. The contractor must ensure appropriate equipment is installed and not base decisions solely on the lowest bid. The contractor needs to be aware of the consequences of poor installation and minimize system effects.
The losses accrued in a system directly affect the system's power consumption while indirectly increasing the energy consumed by other processes. Energy losses in the form of heat equate to higher operating costs.
Because performance conditions are mandated by codes, proper system design, equipment selection, and installation are the most effective means of minimizing inefficiencies and saving energy.
References
- ASHRAE. (2007). ASHRAE handbook—HVAC applications. Atlanta: American Society of Heating, Refrigerating and Air-Conditioning Engineers.
- AMCA International. (2010). ANSI/AMCA standard 99-10, standards handbook. Arlington Heights, IL: Air Movement and Control Association International.
- AMCA International. (2007). AMCA publication 201-02, fans and systems. Arlington Heights, IL: Air Movement and Control Association International.
- AMCA International. (2007). AMCA publication 203-90, field performance measurement of fan systems. Arlington Heights, IL: Air Movement and Control Association International.
Brian Mleziva is an application engineer for centrifugal, vane-axial, and industrial products for Greenheck Fan Corp. His responsibilities include product development, marketing-support materials, and customer service. He has a degree in mechanical engineering from Michigan Technological University.
Did you find this article useful? Send comments and suggestions to Executive Editor Scott Arnold at [email protected].