It is important that professionals involved with smoke control know about the myth of panic. Movies, television, and the press often present an unrealistic image that panicked behavior is common in fire situations. Numerous post-fire studies have shown that panic does not occur often.1,2,3 People usually respond adaptively to a fire incident and often are altruistic in their behavior.
This article will address fire-evacuation analysis related to smoke-control applications. The most common types of smoke-control systems are pressurized stairwells, pressurized elevators, zoned smoke control, and atrium smoke control. Evacuation analysis often is needed for smoke-control systems, but is essential for atrium smoke-control systems that rely on smoke filling. With smoke-filling systems, occupants should have sufficient time to leave an atrium before smoke descends upon them.
During building fires, elevators almost always are taken out of service, and vertical evacuation takes place via stairways. In a few situations, elevators are used for evacuation, but this article will address only vertical evacuation via stairways. (For information about calculating evacuation time via elevators, see “Design of Smoke Control Systems for Elevator Fire Evacuation Including Wind Effects”4 and “Protected Elevators for Egress and Access During Fires in Tall Buildings.”5)
The primary approach to estimating evacuation time consists of a hydraulic analogy that simulates people as fluid particles. This analogy can be generated with and without the consideration of human behavior. (For more detailed information about estimating evacuation time, see “SFPE Handbook of Fire Protection Engineering”1 and “Principles of Smoke Management.”6) However, many computer models can be used to estimate evacuation time with and without the consideration of human behavior. A National Institute of Standards and Technology study examined 28 of these computer models.7
TOTAL EVACUATION TIME
Evacuation time consists of pre-movement time and movement time. For example:
tt = tpm + ռtm
where:
tt = total evacuation time (in minutes)
tpm = pre-movement time (in minutes)
tm = modeled evacuation time for an egress route (in minutes)
ռ = evacuation efficiency
The approach described in this article assumes that people follow a directed route to their destination, typically the outdoors or an area of refuge. Such a directed route does not account for the possibilities of proceeding in the “wrong” direction (e.g., traveling in circles or being blocked by smoke or fire). For this reason, an efficiency factor commonly is added to the modeled evacuation time.
There is no consensus about what value should be used for evacuation efficiency, but 1.5 is the minimum. For many applications, an efficiency value of 2 would be more reasonable. For example, a value of 2 might be considered for a building with two egress paths, one of which might be blocked by smoke or fire.
PRE-MOVEMENT TIME
Pre-movement time is the time from the ignition of a fire to a person's becoming aware of it and deciding to move. There are many ways a person can become aware of a fire. Some common cues of a fire include seeing flame, smoke, or the fire department; feeling heat; smelling smoke; hearing noise or a fire alarm; being told; and loss of electrical power. For a detailed discussion of the ways that occupants become aware of a fire, see “SFPE Handbook of Fire Protection Engineering.”1
People often wait for some time after hearing a fire alarm to respond. Part of the reason for such waiting is experience with false alarms. It is reasonable to expect much less waiting time when people become aware of a fire by seeing fire or smoke.
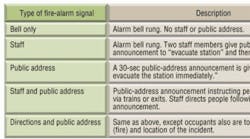
A study of human responses to various types of fire-alarm signals in drills was conducted at mid-afternoon in a London subway station.8 Video cameras recorded individuals' responses, and interviews supplemented the video recording. Five types of alarms were used in the study (Table 1). Alarms were initiated 5 sec after a train arrived at the station. It can be seen from Table 2 that pre-movement time amounted to as much as 9 min for an alarm bell only, but was much less with verbal announcements. However, caution needs to be exercised with the use of verbal announcements, as they involve complex human-behavior issues.
MODELED EVACUATION TIME
Approaches that can be used to calculate evacuation time include component-by-component analysis and constrained-flow analysis. Component-by-component analysis involves a determination of the time it takes for a population to traverse each egress component. The density of flow along each egress component must be determined to measure velocity and flow rate. Component-by-component analysis can be used to analyze complex flow situations involving merging, diverging, and converging flows.
Component-by-component analysis is more complicated and time-consuming than constrained-flow analysis. If a component-by-component analysis is required, a computer-generated evacuation model should be considered.
CONSTRAINED-FLOW ANALYSIS
The constrained-flow approach is appropriate for an egress system that has a point at which a line of waiting people forms. Considering that the constraint is the exterior stairwell door and all occupants start their evacuation simultaneously at time zero, the modeled evacuation time is estimated as:
tm = ta + tc
where:
tm = modeled evacuation time for an egress route (in minutes)
ta = time for first person to arrive at the exterior stairwell door (in minutes)
tc = time for population to pass through the exterior stairwell door (in minutes)
If all stairwell doors are the same width, the constraint will be at the exterior stairwell door. If the width of the exterior door is less than the sum of the widths of the interior stairwell doors that are used for evacuation, the exterior door still is the constraint.
Considering that the first person to reach the exterior stairwell door is walking down the stairs from the floor above, the time to reach the exterior door is about 0.5 min. The time for the population to pass through the exterior stairwell is estimated as:
TABLE 3. The time it takes for a person to pass through the exterior stairwell door depends on the door's width
tc = ßP
where:
ß = time for a person to pass through the exterior stair door (in minutes)
P = population evacuating through the stairs
The time it takes for a person to pass through the exterior stairwell door, ß, depends on the door's width (Table 3).
EXAMPLE CALCULATION
Let's determine the evacuation time for a five-story building with two stairways and 200 people on each floor (Figure 1). The doors leading into and out of the stairways are 32-in. wide. The pre-movement time, tpm, is estimated at 8 min, and the evacuation efficiency, ռ, is taken to be 2.
FIGURE 1. Evacuation paths for a five-story building with two stairways and 200 people on each floor
The people on the first floor would exit directly to the outside without using the stairs. The population of the remaining floors using the two stairways is calculated as:
4(200) = 800 people
It is considered that half of the people would use one stairway, and half would use the other. Therefore, the population using a stairway is P = 400. As seen in Table 3, ß = 0.025 for a 32-in.-wide exterior stairwell door. The time for population to pass through the exterior stair is estimated as:
tc = ßP = 0.025(400) = 10 min
The modeled evacuation time is:
tm = ta + tc = 0.5 + 10 = 10.5 min
The total evacuation time is:
tt = tpm + ռtm = 8 + 2(10.5) = 29 min
SUMMARY
Evacuation time can be estimated by a hydraulic analogy to simulate people as fluid particles. It is important that estimates of evacuation time include pre-movement time and evacuation efficiency. The constrained-flow approach is appropriate for a large number of buildings in which the exterior stairwell door is the flow constraint. For more complex egress routes, a component-by-component analysis can be done, and information about this kind of analysis is available from other sources. For such complicated routes, readers may consider using a computer-evacuation model.
REFERENCES
-
Society of Fire Protection Engineers. (2002). SFPE handbook of fire protection engineering. Quincy, MA: National Fire Protection Association.
-
Quarentelli, E.L. (1979, October). Five papers from the panel session on panic. Paper presented at the Second International Seminar on Human Behavior in Fire Emergencies, Washington, DC.
-
Keating, J. (1982). The myth of panic. Fire Journal, 3, 57-61, 147.
-
Klote, J.H. (1995, April). Design of smoke control systems for elevator fire evacuation including wind effects. Paper presented at Elevators, Fire, and Accessibility, Second Symposium, New York, NY.
-
Bukowski, R.W. (2003, October). Protected elevators for egress and access during fires in tall buildings. Paper presented at the CIB-CTBUH Conference on Tall Buildings, Kuala Lumpur, Malaysia.
-
Klote, J.H., & Milke, J.A. (2002). Principles of smoke management. Atlanta: American Society of Heating, Refrigerating and Air-Conditioning Engineers.
-
Kuligowski, E.D. (2004, June). Review of 28 egress models. Paper presented at the Workshop on Building Occupant Movement During Fire Emergencies, Gaithersburg, MD.
-
Proulx, G., & Sime, J.D. (1991, July). To prevent ‘panic’ in an underground emergency: Why not tell people the truth. Paper presented at the Third International Symposium on Fire Safety Science, Edinburgh, Scotland.
A smoke-control consultant, John H. Klote, DSc, PE, developed and conducts a series of smoke-control seminars for the Society of Fire Protection Engineers. For 19 years, he conducted fire research for the National Institute of Standards and Technology. He is one of the authors of the books “A Guide to Smoke Control in the 2006 IBC” and “Principles of Smoke Management.”
Related Articles:
The True Story
Fire- and Smoke-Damper Control